The ability to stop quickly in response to a hazard is critical to safety. Modern bicycle disk brakes are generally capable of locking the wheels under most conditions. Stopping distance is therefore limited by the point at which wheels skid and by the deceleration at which the rider will pitch-over (go over the handlebars). Skidding occurs when the braking force exceeds the friction between the tires and the road. Better rubber compounds and wider tires with lower pressure will increase this friction. Road conditions such as water and oil on the road will also have a very significant effect on tire friction. The deceleration at which pitch-over occurs depends on the position of the combined center of gravity (CofG) for the cyclist and bike. If the CofG is close to the ground and far behind the front wheel then the stopping distance will be reduced. Under conditions where the stopping distance is limited by friction rather than pitch-over, the optimal distribution of force between the front and rear brake will produce the shortest stopping distance. Anti-lock brakes are a practical way to prevent skidding but electronic braking-pressure distribution system can achieve this optimal distribution of braking force.
In this open access paper, dynamic equations are presented which give the optimal distribution of braking force between the front and rear wheel. When braking momentum causes weight to shift from the rear wheel to the front wheel. The friction force for the rear wheel, therefore, reduces as the total braking force increases. At the point just before pitch-over occurs all of the braking force is due to the front wheel.
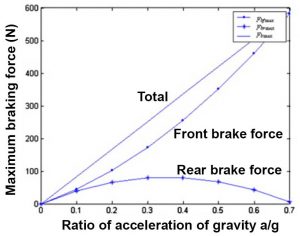
A simple way to increase the force on the rear wheel in relation to the front wheel is to use a smaller disk rotor on the rear wheel. To achieve optimal braking the equations presented in the paper can be used to control an electronic braking-pressure distribution system. This is most likely to be practically implemented in an e-bike which also has electronically controlled regenerative braking.
Abstract:
This paper presents an investigation on the braking performance and safety for a bicycle riding on a straight and an inclined paths. The equations of motion for a wheel model as well as the model for ideal synchronous braking are derived to acquire the shortest braking distance and improve the riding stability. The optimal design of the bicycle braking is obtained based on the simulation results with various bicycle geometries, ratios of brake force, and road friction.
Reference:
“Synchronous brake analysis for a bicycle”
David Lie Cheng-Kuo Sung
Mechanism and machine theory, 2010, Vol.45(4), p.543-554
Let us know what you think